Denoising Diffusion

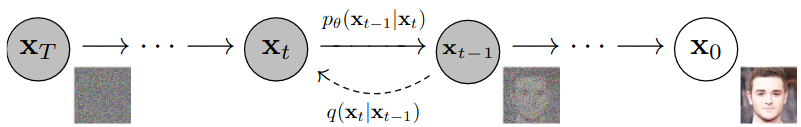
A diffusion probabilistic model is a parameterized Markov chain trained using variational inference to produce samples that match data after a finite time. Transitions of the chain are learned to reverse the diffusion process, where noise is gradually added in the opposite direction until the signal is destroyed.

These are latent variable models of the form $p_{\theta}(x_0) := \int p_{\theta}(x_{0:T}) \ dx_{1:T}$ where the latent space $x_1, ..., x_T$ has the same dimensionality as the data $x_0 \sim q(x_0)$. The joint distribution $p_{\theta}(x_{0:T})$ is called the reverse process and is defined with learned Gaussian transitions.

\begin{align*} p_{\theta}(x_{0:T}) &:= p(x_T) \prod_{t=1}^T p_{\theta}(x_{t-1} | x_t) \\ p_{\theta}(x_{t-1} | x_t) &:= \mathcal{N}(x_{t-1}; \mu_{\theta}(x_t, t), \Sigma_{\theta}(x_t, t)) \end{align*}

The unique quality of diffusion is the forward process where the approximate posterior $q(x_{1:T}|x_0)$ gradually adds Gaussian noise to the data according to a variance schedule $\beta_1, ..., \beta_T$.

\begin{align*} q(x_{1:T}|x_0) &:= \prod_{t=1}^T q(x_t | x_{t-1}) \\ q(x_t | x_{t-1}) &:= \mathcal{N}(x_t; \sqrt{1 - \beta_t} \ x_{t-1}, \ \beta_t I) \end{align*}

Training is performed by optimizing the variational bound on negative log likelihood.

$$ L := \mathbb{E}[-log \ p_{\theta}(x_0)] \leq \mathbb{E} \left[ -log \frac{p_{\theta}(x_{0:T})}{q(x_{1:T} | x_0)} \right] = \mathbb{E} \left[ -log \ p(x_T) - \sum_{t \leq 1} log \frac{p_{\theta}(x_{t-1} | x_t)}{q(x_t | x_{t-1})} \right] $$

The forward process variances can be learned or held constant as tunable hyperparameters. Efficient training is possible by optimizing random terms of L rewritten as:

$$ \mathbb{E}_q \left[ \underbrace{D_{KL}(q(x_T | x_0) \ || \ p(x_T))}_{L_T} + \sum_{t>1} \underbrace{D_{KL}(q(x_{t-1}|x_t, x_0) \ || \ p_{\theta}(x_{t-1}|x_t))}_{L_{t-1}} - \underbrace{log \ p_{\theta}(x_0 | x_1)}_{L_0} \right] $$